
|
| ļ¬®ņĀü ļ░Å ļ▓öņ£ä Aims and Scope |
| ņĀĆļäÉ ņĀĢļ│┤ About the Journal |
| ĒÄĖņ¦æņ£äņøÉĒÜī Editorial Board |
| Open Access |
| ĒÄĖņ¦æĻĄŁ Editorial Office |


|
| ļ¬®ņĀü ļ░Å ļ▓öņ£ä Aims and Scope |
| ņĀĆļäÉ ņĀĢļ│┤ About the Journal |
| ĒÄĖņ¦æņ£äņøÉĒÜī Editorial Board |
| Open Access |
| ĒÄĖņ¦æĻĄŁ Editorial Office |

AbstractLa/Ce-partially double-filled and Co-charge-compensated (La1-zCez)0.8Fe4-xCoxSb12 skutterudites were synthesized, and their thermoelectric properties were studied by varying the filling ratio and charge compensation. X-ray diffraction analysis revealed that the matrix phase was skutterudite and a secondary phase was determined to the marcasite FeSb2. However, the formation of marcasite could be inhibited by increasing the Co content. Rare-earth antimonides, including LaSb2 and CeSb2, which were formed in fully filled La1-zCezFe4-xCoxSb12, were not found after La/Ce partial filling. La/Ce filling and Co substitution were confirmed by the decrease in lattice constants, from 0.9137 to 0.9099 nm, with increasing Ce and Co contents. Electrical conductivity showed negative temperature dependence, indicating metallic or degenerate semiconductor characteristics. Intrinsic conduction resulted in the maximum Seebeck coefficient at temperatures between 723 and 823 K. As the Co-substitution and Ce-filling contents increased, the Seebeck coefficient increased, while electrical and thermal conductivities decreased. This was considered to be due to difference in the valences of La3+ and Ce3+/4+ and the increase in carrier concentration caused by Co charge compensation. However, because they had similar atomic masses and ionic radii, the effects of the La/Ce filling ratio were not significant. Instead, Co charge compensation had the dominant effect on thermoelectric properties. The maximum Seebeck coefficient of 165.4 ┬ĄVK-1 was obtained for (La0.25Ce0.75)0.8Fe3CoSb12 at 823 K, and the highest electrical conductivity of 2.27 ├Ś 105 S m-1 was achieved for (La0.75Ce0.25)0.8Fe4Sb12. (La0.25Ce0.75)0.8Fe3CoSb12 exhibited the lowest thermal conductivity of 2.15 W m-1K-1 at 523 K and (La0.75Ce0.25)0.8Fe3.5Co0.5Sb12 showed the highest power factor of 2.53 mW m-1 K-2 at 723 K. The maximum dimensionless figure of merit, ZTmax = 0.71, was achieved at 723 K for (La0.75Ce0.25)0.8Fe3CoSb12.
1. IntroductionSkutterudites are the most suitable thermoelectric material for exploiting the phonon-glass and electron-crystal concept [1]. They are also some of the best thermoelectric materials for thermoelectric power generation applications, because they operate efficiently at waste heat temperatures between 500ŌĆō900 K [2-5]. Skutterudite has the basic structure of 8MX3, with two large voids per unit cell, where M represents group AVIII elements (Fe, Co, Ni, Ru, Rh, Pd, Os, Ir, Pt) and X stands for group BV elements (P, As, and Sb). Filled skutterudites, which incorporate phonon scattering centers, have been studied in efforts to improve thermoelectric performance. The guest atoms (R: filler or rattler) in the voids are filled with skutterudite [6-8]. RFe4Sb12 is usually used for the p-type filled skutterudite, but [Fe4Sb12] is not stable due to deficient valence electrons, and requires four additional electrons to stabilize the skutterudite phase [9,10]. Skutterudite can be formed as R4+[Fe4Sb12]4- by filling the voids, but most elements incorporated as fillers exist as valences of R2+ and R3+. As a result, the number of valence electrons is insufficient [11], and charge compensation is needed in the form of R2+[Fe3NiSb12]2- or R3+[Fe3CoSb12]3- by substituting Ni or Co at the Fe site [12].
Filling the voids in the skutterudite structure is a very effective method for reducing lattice thermal conductivity [3,13-15] because each filler atom acts as a phonon scattering center with a specific resonant frequency [16]. Alkali, alkaline-earth, and rare-earth metals are commonly used as the filling elements. Rare-earth elements, with atomic masses heavier than alkali or alkaline-earth elements, lead to lower lattice thermal conductivity because they promote phonon scattering of lower resonant frequencies [17]. Compared to a single-filled skutterudite, lattice thermal conductivity can be reduced further by filling with two or more kinds of atoms, because they accommodate a broader spectrum of phonon frequencies [16,18]. However, some studies have reported that double- or multiple-filled skutterudites cannot be completely filled [19-21].
In our previous study [22], La1-zCezFe4-xCoxSb12 specimens produced (La,Ce)Sb2 phases because the La/Ce double filling was beyond the filling fraction limit (FFL). In this study, to prevent (La,Ce)Sb2 phase formation, La/Ce-partially-double-filled and Co-substituted skutterudites were prepared, and the effects of charge compensation on the thermoelectric properties of (La1-zCez)0.8Fe4-xCoxSb12 were examined.
2. Experimental Procedure(La1-zCez)0.8Fe4-xCoxSb12 skutterudites with various filling ratios (z = 0.25 or 0.75) and charge compensation levels (x = 0, 0.5, and 1) were prepared. Base elements of Fe (purity 99.95%, Cerac) and Sb (purity 99.999%, LTS), filling elements of La (purity 99.9%, Kojundo) and Ce (purity 99.9%, Sigma Aldrich), and the charge-compensating element, Co (purity 99.95%, Alfa Aesar), were used to synthesize the skutterudite specimens. Each element was weighed to the stoichiometric ratio and fused at 1323 K for 10 h in an vacuum-sealed quartz ampoule (inner diameter: 10 mm) that was coated inside with carbon, and the ingot was quenched in water. After replacing with another larger quartz tube (inner diameter: 11 mm) to prevent the destruction of the quartz tube due to thermal expansion, the ingot was vacuum-sealed again and then annealed at 873 K for 24 h to stabilize and homogenize the skutterudite phase. The obtained ingot was pulverized, and then its powder was charged into a graphite mold, followed by hot pressing under a pressure of 70 MPa at 898 K for 1 h in a vacuum.
X-ray diffraction (XRD; Bruker, Cu K╬▒ radiation) was employed to identify the phases of the hot-pressed specimens. Scanning electron microscopy (SEM; FEI) and energy-dispersive spectroscopy (EDS; Oxford) were used to observe the microstructure and analyze elemental distribution. The Seebeck coefficient (╬▒) and electrical conductivity (Žā) were measured using ZEM-3 (Advance Riko) equipment. The thermal conductivity (╬║ = Dcpd) was estimated after measuring the thermal diffusivity (D), specific heat (cp), and density (d) using the TC-9000H (Advance Riko) system. The power factor (PF = ╬▒2Žā) and dimensionless figure of merit (ZT = ╬▒2ŽāT╬║-1) were determined from the obtained Seebeck coefficient, electrical conductivity, and thermal conductivity.
3. Results and DiscussionThe XRD patterns of the hot-pressed (La1-zCez)0.8Fe4-xCoxSb12 specimens are presented in Fig 1. All the diffraction peaks matched the ICDD reference data (PDF# 56-1123) for the skutterudite phase, and no rare-earth compounds, including LaSb2 and CeSb2, were identified. As noted, in our previous study [22], (La,Ce)Sb2 phases were found in fully filled La1-zCezFe4-xCoxSb12, but in this study, these phases did not exist in the partially filled (La1-zCez)0.8 Fe4-xCoxSb12 because the filling fraction of 0.8 did not exceed the FFL. (La1-zCez)0.8Fe4Sb12 specimens without the Co substitution (charge compensation) contained the marcasite FeSb2 (PDF# 70-3985) as a secondary phase. However, as the charge-compensating amount of Co was increased, the intensities of the marcasite diffraction peaks decreased, and thus it was expected that the formation of the secondary phase would decrease. Detailed microstructural and compositional analyses were performed for verification.
SEM images and EDS line scans of (La1-zCez)0.8Fe4-xCoxSb12 are shown in Fig 2. All of the specimens consisted of skutterudite phase (bright region) and marcasite phase (dark region), consistent with the XRD results. The formation of marcasite was suppressed with increasing Co content, which implies that Co charge compensation stabilized the skutterudite phase. Joo et al. [22] reported that (La,Ce)Sb2 phases were observed, together with the FeSb2 phase, in fully filled La1-zCezFe1-xCoxSb12 specimens. However, in the present study, partial filling did not exceed the FFL, so the (La,Ce)Sb2 phases did not form.
Table 1 presents the chemical and physical properties of (La1-zCez)0.8Fe4-xCoxSb12. There was no significant difference between the nominal and actual compositions. It was confirmed that the constituents were not volatilized or oxidized during the melting and sintering processes. The hot-pressed specimens exhibited relative densities of 96.1ŌĆÆ99.6% compared with the theoretical density. Because the ionic radius of Co2+ (0.167 nm) is smaller than that of Fe3+ (0.172 nm) [23], the lattice constant was decreased by Co substitution for Fe; the lattice constant decreased, from 0.9136ŌĆÆ0.9137 to 0.9099ŌĆÆ0.9109 nm, with increasing Co content. Variation in the lattice constant with increased La/Ce filling ratio was not significant because the ionic radii of La (0.136 nm) and Ce (0.134 nm) are very similar [24]; as Ce content increased, the lattice constant slightly decreased.
The electrical conductivity of (La1-zCez)0.8Fe4-xCoxSb12 is presented in Fig 3. The electrical conductivity exhibited a negative temperature dependence, that is, it decreased with increasing temperature, which means that all of the specimens behaved like metallic or degenerate semiconducting materials. Each specimen exhibited a maximum electrical conductivity at 323 K; (2.16ŌĆÆ2.27) ├Ś 105 S m-1 for the Cofree specimens and (0.84ŌĆÆ1.30) ├Ś 105 S m-1 for the Cosubstituted specimens. The electrical conductivity decreased significantly when Co was substituted for Fe. This was attributed to the carrier concentration, which was expected to decrease due to charge compensation. Joo et al. [22] reported that fully filled and Co-compensated La1-zCezFe4-xCoxSb12 specimens had high carrier concentrations of (1.07ŌĆÆ1.87) ├Ś 1021 cm-3 and high electrical conductivity values of (1.10ŌĆÆ1.76) ├Ś 105 Sm-1 at 323 K. However, in this study, (La0.75Ce0.25)0.8Fe4Sb12 exhibited the highest electrical conductivity of 2.27 ├Ś 105 Sm-1 at 323 K. The reason the partially-filled specimens had higher electrical conductivities was because of the increased charge carrier (hole) concentration, resulting from the reduced supply of excess electrons. In addition, the electrical conductivity decreased with increasing Ce content, due to the difference in valences between La3+ and Ce3+/4+.
The Seebeck coefficient of (La1-zCez)0.8Fe4-xCoxSb12 is shown in Fig 4. In the temperature range 323ŌĆÆ823 K, the Seebeck coefficient exhibited positive values, thereby confirming p-type conduction. The Seebeck coefficient of a p-type semiconductor can be expressed by MottŌĆÖs equation [25]:
In this study, as the temperature increased, the Seebeck coefficient increased, reaching maximum values in the temperature range 723ŌĆÆ823 K. In addition, as the Co content increased, the Seebeck coefficient increased, and the carrier concentration was expected to decrease due to charge compensation. This was consistent with the observation of variation in electrical conductivity shown in Fig 3. Therefore, the increased Seebeck coefficient resulted from the decreased carrier concentration.
A minimum Seebeck coefficient of 124.5 ╬╝V K-1 was obtained at 823 K for (La0.75Ce0.25)0.8Fe4Sb12, but the maximum Seebeck coefficient of 165.4 ╬╝V K-1 was achieved at 823 K for (La0.25Ce0.75)0.8Fe3CoSb12. The Seebeck coefficients of the fully filled La1-zCezFe4-xCoxSb12 specimens exhibited maximum values at 723ŌĆÆ823 K, and La0.25Ce0.75Fe3CoSb12 exhibited the highest value of 164.1 ╬╝V K-1 at 823 K [22]. However, in this study, the Seebeck coefficient did not significantly increase with partial filling. Therefore, it was confirmed that the change in the Seebeck coefficient was more affected by Co-charge compensation than by the filling fraction and La/Ce ratio.
The power factor of (La1-zCez)0.8Fe4-xCoxSb12 is presented in Fig 5. Because electrical conductivity is proportional to carrier concentration, while the Seebeck coefficient is inversely proportional to carrier concentration, there is a trade-off between these two parameters. In addition, these two parameters exhibit different temperature dependences. Therefore, there is a maximum power factor that can be obtained with an optimum carrier concentration, at a specific temperature. In this study, the power factor increased with increasing temperature, and the maximum power factor was 823 K for the Co-free specimens. However, the Cosubstituted specimens exhibited a maximum power factor at 723 K. The power factor increased as the La content increased, with constant Co content. Partial filling was expected to improve the power factor by enhancing electrical conductivity through hole donation, but electrical conductivity and the Seebeck coefficient did not change significantly, resulting in a slightly lower power factor compared with fully filled specimens. In this study, the power factor ranged from 2.25 to 2.53 mW m-1 K-2 at 723ŌĆÆ823 K, and (La0.75Ce0.25)0.8 Fe3.5Co0.5Sb12 exhibited a maximum value of 2.53 mW m-1K-2 at 723 K. The fully filled La0.75Ce0.25Fe3.5Co0.5Sb12 achieved a maximum power factor of 2.79 mW m-1 K-2 at 723 K [22].
The thermal conductivity of (La1-zCez)0.8Fe4-xCoxSb12 is shown in Fig 6. Thermal conductivity (╬║) consists of electronic thermal conductivity (╬║E) from the contribution of charge carriers, lattice thermal conductivity (╬║L) from the contribution of phonons, and bipolar thermal conductivity (╬║B) from the contribution of bipolar conduction. In this study, ╬║B was ignored, since it was assumed that the carrier concentration was very high (degenerate semiconductors), and ╬║E was estimated using the Wiedemann-Franz law (╬║E = LŽāT) [26]. In general, L (Lorenz number) has a range of (1.45ŌĆÆ2.44) ├Ś 10-8 V2 K-2 and here was taken to be L = 2.0 ├Ś 10-8 V2 K-2.
The thermal conductivity is shown in Fig 6(a). The specimens showed thermal conductivities between 2.15 and 4.17 Wm-1 K-1 at 323ŌĆÆ823 K. As with the other thermoelectric parameters, the change in thermal conductivity was not significantly affected by the La/Ce filling ratio, but was highly dependent on Co content. Thermal conductivity was significantly reduced as the amount of Co-substitution increased. The lowest thermal conductivity of 2.15 W m-1 K-1 was obtained at 523 K for (La0.25Ce0.75)0.8Fe3CoSb12. Electronic thermal conductivity decreased with increasing Co content (Fig 6(b)). This was due to the decrease in carrier concentration caused by the charge compensation of Co.
Each specimen exhibited the lowest electronic thermal conductivity of 0.53ŌĆÆ1.49 W m-1 K-1 at 323 K. Compared with the electrical conductivity change shown in Fig 3, the opposite temperature dependence occurred, but the composition (filling and substitution) dependence behavior remained the same. The minimum electronic thermal conductivity of 0.53 W m-1 K-1 was obtained at 323 K for (La0.25Ce0.75)0.8Fe3CoSb12. The lowest lattice thermal conductivity of 1.18ŌĆÆ1.62 W m-1 K-1 at 623 K was observed in all specimens (Fig 6(c)). As the Co content increased, lattice thermal conductivity decreased because of the enhanced phonon scattering by impurities. (La0.25Ce0.75)0.8Fe3CoSb12 exhibited the lowest lattice thermal conductivity of 1.18 W m-1 K-1 at 623 K. The lattice thermal conductivity of the fully filled La0.75Ce0.25Fe3.5Co0.5Sb12 was greatly reduced and exhibited the lowest value of 0.47 W m-1 K-1 at 723 K [22]. The lattice thermal conductivity of the partially filled specimens was relatively high compared to those of the fully filled specimens. The lattice thermal conductivity was expected to be reduced by intensifying phonon scattering when using heavy La and Ce with small ionic radii as filling elements. However, the enhancement in phonon scattering was negligible because La has a very similar atomic mass and ionic radius to Ce. As a result, the lattice thermal conductivity could not be lowered by partial filling. However, electronic thermal conductivity was decreased by Co-charge compensation, so that the total thermal conductivity of the partially filled specimens was similar to that of fully filled specimens.
The dimensionless figures of merit (ZT) of (La1-zCez)0.8 Fe4-xCoxSb12 are presented in Fig 7. As temperature increased, ZT values increased; the Co-free specimens showed maximum ZT values at 823 K, but the temperature at which the ZT value peaked was reduced to 723 K by Co-charge compensation. The highest ZT value of 0.71 was obtained at 723 K for (La0.75Ce0.25)0.8Fe3CoSb12.
Previously, slightly higher values of ZT = 0.77 at 723 K and ZT = 0.79 at 823 K were reported for fully filled La0.75Ce0.25Fe3.5Co0.5Sb12 [22]. The partially filled specimens exhibited slightly lower ZT values than fully filled specimens. However, Co-charge compensation reduced the temperature, resulting in a maximum ZT of 100 K, which is considered useful and practical for a thermoelectric material in the mid-low temperature range.
In this study, La and Ce were used with the aim of suppressing secondary phase formation by partial double filling, and to maximize the power factor (optimize carrier concentration) through Co-charge compensation. In addition, a reduction in lattice thermal conductivity was expected due to phonon scattering, with improved thermoelectric performance. However, the improvement in phonon scattering due to partial double filling was negligible; thus, La/Ce partial double filling was not effective for improving thermoelectric performance. Compared with our previous studies on partially double-filled p-type skutterudites, ZT = 0.79 at 723 K was obtained for (La0.25Pr0.75)0.8Fe3.5Co0.5Sb12 [27], ZT = 0.76 at 723 K was achieved for (La0.25Nd0.75)0.8Fe3CoSb12 [28], ZT = 0.84 at 623 K was reported for (Ce0.75Pr0.25)0.8Fe3CoSb12 [29], and ZT = 0.87 at 723 K was attained for (Ce0.75Nd0.25)0.8Fe3CoSb12 [30].
4. ConclusionsP-type (La1-zCez)0.8Fe4-xCoxSb12 skutterudites were prepared using encapsulated melting followed by annealing and hot pressing. Phases, microstructures, and thermoelectric properties were examined as a function of variations in La/Ce partial double filling and Co-charge compensation. A matrix of skutterudite phase and a secondary phase of marcasite was also observed in the hot-pressed specimens. However, rareearth antimonides, including LaSb2 and CeSb2 phases, were not formed because the La/Ce filling fractions of the partially double-filled specimens were within the FFL. In addition, it was observed that the amount of marcasite was reduced by Co-substitution for Fe. As Co-charge compensation increased, the electrical conductivity decreased, while the Seebeck coefficient and thermal conductivity increased. However, variation in the La/Ce filling ratio did not significantly affect thermoelectric performance. This was because La and Ce have very similar atomic mass and ionic radius, which did not effectively enhance phonon scattering by partial double filling; thus, lattice thermal conductivity was not reduced compared with that of the fully filled specimens. As a result, the highest power factor of 2.53 mW m-1 K-2 was obtained at 723 K for (La0.75Ce0.25)0.8Fe3.5Co0.5Sb12, and a ZTmax of 0.71 was achieved at 723 K for (La0.75Ce0.25)0.8Fe3CoSb12. The substitution of Co for Fe improved the ZT values of the ptype skutterudites by charge compensation, and it was confirmed that partial double filling using filler elements with large differences in atomic mass and ionic radius may be more effective for improving thermoelectric performance.
AcknowledgmentsThis study was supported by Hanseo University in 2019 and by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education (NRF-2019R1A6A1A11055660) and by the Basic Science Research Capacity Enhancement Project (National Research Facilities and Equipment Center) through the Korea Basic Science Institute funded by the Ministry of Education (Grant No. 2019R1A6C1010047).
Fig.┬Ā6.Temperature dependence of the thermal conductivity of (La1ŌłÆzCez)0.8Fe4ŌłÆxCoxSb12: (a) total thermal conductivity, (b) electronic thermal conductivity, and (c) lattice thermal conductivity. 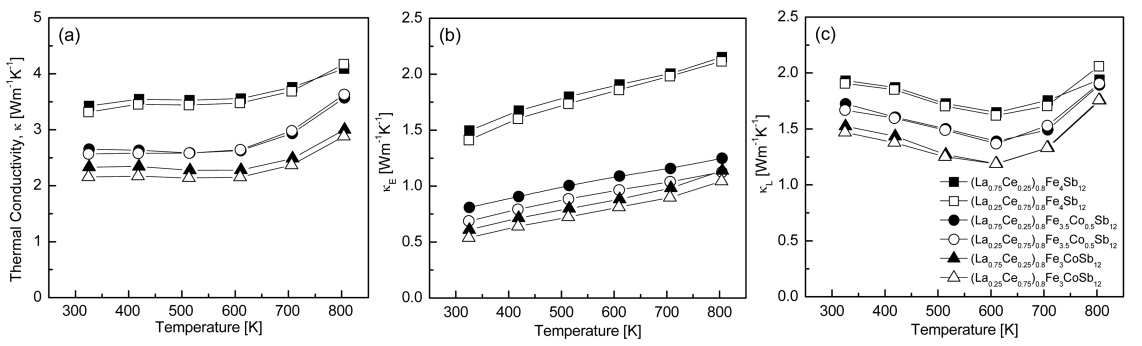
Fig.┬Ā7.Temperature dependence of the dimensionless figure of merit for (La1ŌłÆzCez)0.8Fe4ŌłÆxCoxSb12. 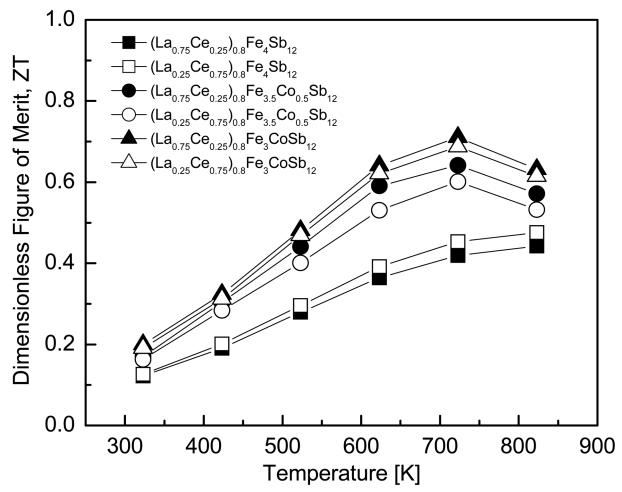
Table┬Ā1.Chemical compositions, relative densities, and lattice constants of (La1ŌłÆzCez)0.8Fe4ŌłÆxCoxSb12. REFERENCES1. G. A. Slack, CRC Handbook of Thermoelectrics, In : D. M. Rowe, editor. pp. 407CRC Press, US (1995).
4. B. C. Sales, D. Mandrus, B. C. Chakoumakos, V. Keppens, and J. R. Thompson, Phys. Rev. B. 56, 15081 (1997).
8. D. Mandrus, A. Migliori, T. W. Darling, M. F. Hundley, E. J. Peterson, and J. D. Thompson, Phys. Rev. B. 52, 4926 (1995).
10. J. Leszczynski, V. D. Ros, B. Lenoir, A. Dauscher, C. Candolfi, P. Masschelein, J. Hejtmanek, K. Kutorasinski, J. Tobola, R. I. Smith, C. Stiewe, and E. Muller, J. Phys. D. 46, 495106 (2013).
11. B. X. Chen, J. H. Xu, C. Uher, D. T. Morelli, G. P. Meisner, J. P. Fleurial, T. Caillat, and A. Borshchevsky, Phys. Rev. B. 55, 1476 (1997).
12. S. Ballikaya, N. Uzar, S. Yildirim, H. Chi, X. L. Su, G. J. Tan, X. F. Tang, and C. Uher, J. Electron. Mater. 42, 1622 (2013).
14. L. D. Chen, T. Kawahara, X. F. Tang, T. Goto, T. Hirai, J. S. Dyck, W. Chen, and C. Uher, J. Appl. Phys. 90, 1864 (2001).
17. Z. Chen, J. O. Yang, R. H. Liu, L. L. Xi, W. Q. Zhang, and J. Yang, J. Electron. Mater. 42, 2492 (2013).
18. C. Uher, Thermoelectrics Handbook, In : D. M. Rowe, editor. pp. 527CRC Press, US (2006).
20. G. Rogl, A. Grytsiv, M. Falmbigl, E. Bauer, P. Rogl, M. Zehetbauer, and Y. Gelbstein, J. Alloys Compd. 537, 242 (2012).
24. J. Leszczynski, V. D. Ros, B. Lenoir, A. Dauscher, C. Candolfi, P. Masschelein, J. Hejtmanek, K. Kutorasinski, J. Tobola, R. I. Smith, C. Stiewe, and E. M├╝ller, J. Appl. Phys. 46, 495106 (2013).
26. C. Kittel, Introduction to Solid State Physics, 6th ed. pp. 152John Wiley & Sons, NewYork (1986).
|
|
|||||||||||||||||||||||||||||||||||||||