Numerous studies on eco-friendly energy-production technologies have been conducted in various fields [1]. In particular, thermoelectric technology can be used for reversible energy conversion—from heat to electricity based on the Seebeck and Peltier effects, respectively [2,3]. Thermoelectric performance is evaluated using the dimensionless thermoelectric figure of merit, zT = S²σT/κ_tot, where S, σ, κ_tot and T are the Seebeck coefficient, electrical conductivity, total thermal conductivity, and absolute temperature, respectively. Generally, κ_tot is divided = κ_ele and κ_latt, where κ_ele and κ_latt are electrical and lattice thermal conductivities, respectively. The most important goal of research on thermoelectric materials is to en_Hance zT. However, κ_ele and σ are closely related to each other according to the Wiedemann-Franz law (κ_ele = L · σ · T, where L is the Lorenz number) [4]; consequently, en_Hancing zT is challenging. Therefore, zT can be improved by either increasing the power factor (S²σ, PF) or by decreasing κ_tot. Skutterudites are typical thermoelectric materials with high PF. CoSbCoSb₃-based skutterudites have a relatively high κ_tot of 3W/mK or more and a high PF of approximately 5 mW/mK² [5]. Skutterudites show excellent thermoelectric performance at high temperatures, but relatively poor performance at low temperatures. Therefore, skutterudites are unsuitable for wearable devices or vehicle applications. The most effective stratE_gy for improving zT at low temperatures is to reduce κ_tot [6,7]. Chalcogenides have a very low κ_tot owing to their weak van der Waals bonding between atomic layers; thus, they can be potential thermoelectric materials with a high zT even at room temperature [8].

Chalcogenides are being actively studied as modules for various devices such as wearable devices and generators for vehicles [9,10]. Defect engineering, such as doping and nanostructuring, is an effective approach for reducing κ_latt by increasing point-defect phonon scattering [11-13]. This stratE_gy has been adopted in many studies to en_Hance zT in chalcogenides [13-17]. Rhyee et al. reported that In₄Se_2.35 exhibited a very high zT value of 1.48 at 705 K via self-doping by Se deficiency [13]. Qin et al. synthesized Mndoped Bi_0.5Sb_1.5Te₃ and a maximum zT of ~1.3 was achieved for Mn_0.0075Bi_0.5Sb_1.4925Te₃ at 430 K [15].

However, the thermoelectric performance of rhenium chalcogenide compounds has not been extensively investigated. According to density functional theory calculations by Hafeez et al. [18], ReS₂ and ReSe₂ have different band gaps:1.58 eV (1.50 eV) for monolayer (bulk) ReS₂ and 1.32 eV (1.26 eV) for monolayer (bulk) ReSe₂. Sreeparvathy reported that ReX₂ (x = S and Se) has flat bands aligned in both the valence and conduction bands, which contribute to the enhancement of S [19]. Sreeparvathy also showed that ReS₂ has the potential to have a large S of 540-600 μV/K at 300 K. Re₂Te₅, a rhenium chalcogenide, does not have a layered structure but has a complex orthorhombic (space group: Pbca [61]) crystal structure with 84 atoms ([Re₂4] and [Te₆₀]) per unit cell. These atoms exhibit a cluster-type Chevrel phase, with [Re6] surrounded by [Te8] [20-22].

One of the structural properties of the Chevrel phase is the presence of four large vacancies. This causes scattering of phonons, effectively reducing κ_latt. Inevitably, κ_tot of Re₂Te₅ is 1.3 W/mK which is as low as that of chalcogenides which have layered structures [21]. Further, Caillat et al. reported that rattling was observed in elements doped into vacancies, resulting in reduced κ_tot due to increasing phonon scattering [23]. Therefore, the application of defect engineering to Re₂Te₅ is a reasonable approach for improving thermoelectric performance.

In this study, the thermoelectric transport properties of Se-doped Re₂Te₅ samples were investigated. We synthesized a series of ReTe_5-xSe_x (x = 0, 0.2, 1, and 2) samples. The electrical and thermal transport properties of the samples were investigated, and Hall measurements were conducted to analyze the electrical transport properties of the samples in detail. The density-of-state effective mass was calculated from the measured parameters. zT was evaluated to determine the optimum composition for Se-doped Re₂Te₅.

A series of Re₂Te_5-xSe_x (x = 0, 0.2, 1, and 2) samples were stoichiometrically synthesized using a conventional solidstate reaction process. High-purity element Te (99.999%), Se (99.999%), and Re (99.999%) powders were mixed and loaded in a vacuum quartz tube. The loaded vacuum quartz tube was then heated to 950°C for 6 hours and then maintained for 70 hours. After heating, the samples were cooled to room temperature in a furnace. The synthesized Sedoped Re₂Te₅ samples were pulverized into powder by highenergy ball milling (SPEX 8000D, SPEX). The powder samples were placed in graphite molds and cold-pressed to form the green bodies. The samples were sintered using spark plasma sintering (SPS-1030, Sumitomo Coal Mining Co., Ltd.) under vacuum at 850°C for 10 min under 70 MPa. The crystal structures of the samples and the presence of impurities were identified using X-ray diffraction (XRD, D8 Discover, Bruker) analysis. Furthermore, σ and S were measured simultaneously using a thermoelectric-property measurement system (ZEM-3, Advanced-Riko) in the temperature range of 300-880 K in a He atmosphere. The error margins for σ and S were less than 3% and 5%, respectively.

The Hall carrier concentrations (n_H) and Hall carrier mobilities (μ_H) were measured using a Hall measurement system (HMS5300, Ecopia) under a 0.548 T magnetic field. The κ_tot value of each sample was calculated using the density (ρ_s), heat capacity (Cp), and thermal diffusivity (α). ρ_s was considered to be the theoretical density of orthorhombic Re₂Te₅ (8.423 g/cm³ [2]). The Cp of each sample was measured by differential scanning calorimetry (DSC8000, Perkin Elmer). The α value of each sample was measured by laser flash analysis (LFA457, Netzsch). The error margin for α was less than 7%. The zT values of the samples were calculated based on measured data.

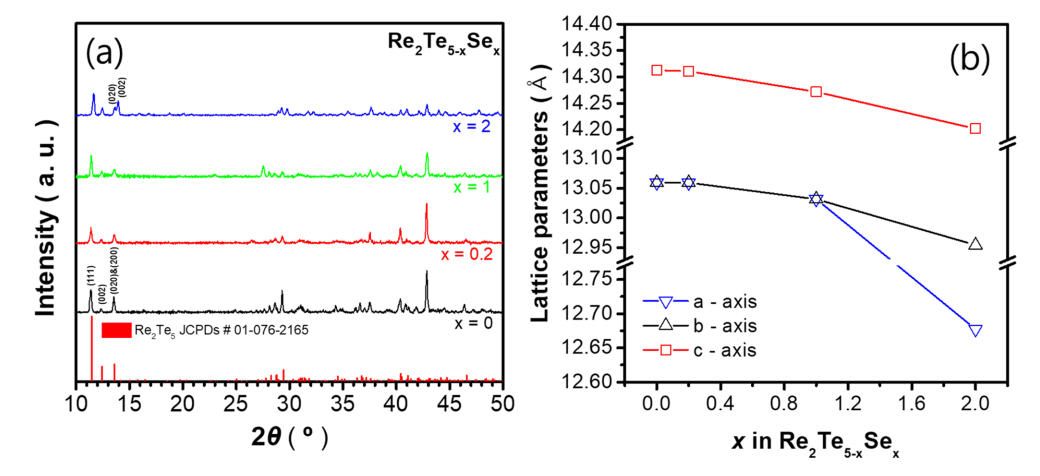
Figures 1(a) and 1(b) show the XRD patterns and calculated lattice parameters of the series of Re₂Te_5-xSe_x (x = 0, 0.2, 1, and 2) samples, respectively. As shown in Figure 1(a), single orthorhombic Re₂Te₅ phases were synthesized without impurities. The (200) and (020) diffraction peaks for the samples with x = 0, 0.2, and 1 appeared as a single peak, and the calculated lattice parameters, a and b of these samples were almost identical. However, for the sample with x = 2, the (200) and (020) peaks were separated. Therefore, the calculated lattice parameters, a and b for x = 2 exhibited significantly different values of 12.68 and 12.95 Å, respectively. The lattice parameters along the three axes gradually decreased with increasing Se doping content, which is attributed to the difference in ionic radii between Se²⁻ (184 pm) and Te²⁻ (207 pm). Therefore, this result confirms that Se atoms were successfully substituted at Te sites.

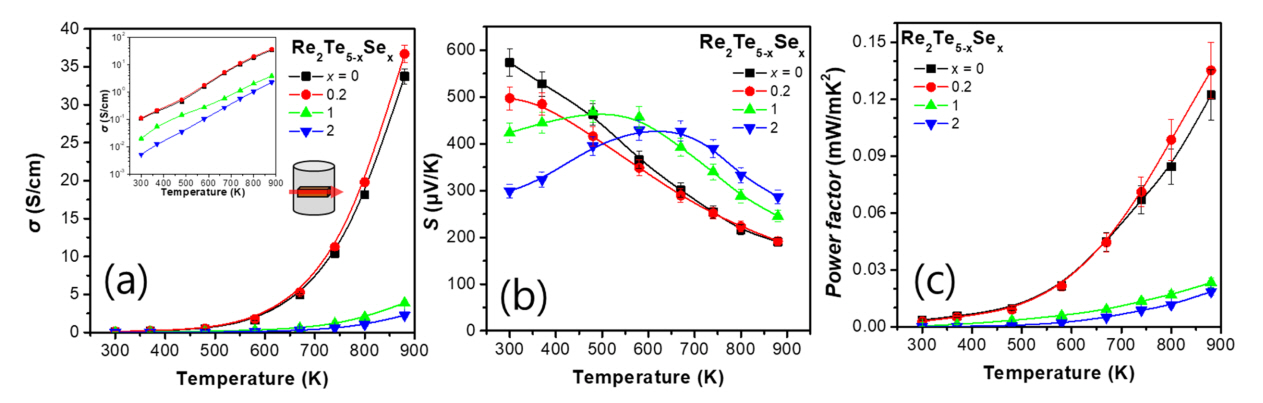
Figure 2 shows the thermoelectric transport properties measured perpendicular to the pressing axis. As shown in Figure 2(a), σ for the samples with x = 0, 0.2, 1, and 2 were 0.106, 0.112, 0.020, and 0.005 S/cm at 300 K, respectively. All the samples exhibited typical semiconductor behavior, and σ_increased to 33.74, 36.71, 3.88, and 2.25 S/cm at 880 K for Re₂Te_5-xSe_x with x = 0, 0.2, 1, and 2, respectively. The maximum σ value was observed for Re₂Te_5-xSe_x with x = 0.2. Figure 2(b) shows the temperature dependence of S for the samples. At 300 K, the S values were 574, 497, 424, and 299 μV/K for Re₂Te_5-xSe_x with x = 0, 0.2, 1, and 2, respectively; at 300 K S decreased gradually with increasing x.

Generally, the magnitude of S increases when σ decreases because of the trade-off relationship between S and σ. However, the S of the samples with x = 1 and 2 at 300 K decreased despite the decrease in σ of these samples. This result can be explained by the bipolar effect. The samples with x = 1 and 2 initially increased with T and then decreased following their maximum values at approximately 580 K, suggesting that bipolar excitation dominates the transport [25]. Therefore, the relationship between the measured S completely reversed at 880 K; the values of S were 190, 192, 245, and 286 for x = 0, 0.2, 1, and 2, respectively at 880 K.

The PF values of the samples calculated from the measured σ and S values are shown in Figure 2(c). The PF values of the samples with x = 0 and 0.2 are very similar up to 670 K, but at T > 670 K, the PF value of the sample with x = 0.2 is higher than that of the sample with x = 0. Therefore, a maximum PF of 0.135 mW/mK² was achieved for x = 0.2 at 880 K. However, the samples with x = 1 and 2 exhibited very low PF values of 0.023 and 0.019 mW/mK² at 880 K, respectively. The decrease in PF for these samples is attributed to the reduction in σ and the small increase in S due to the amplified bipolar effect.

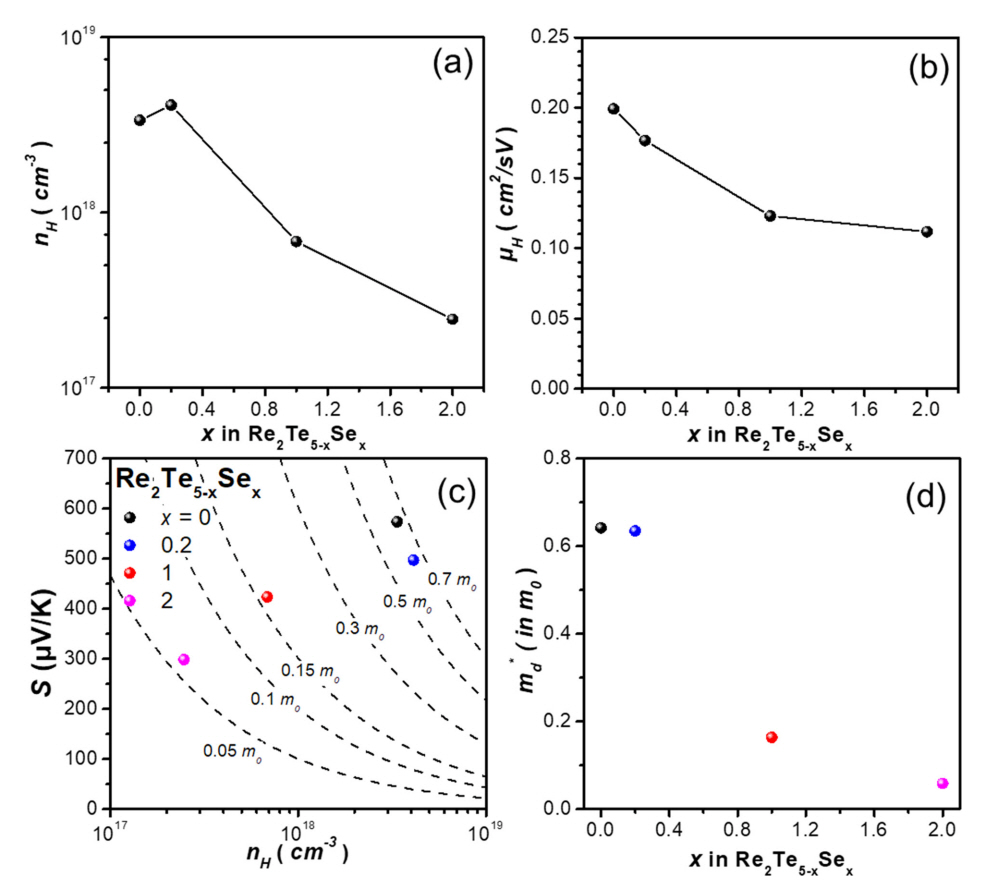
Figures 3(a) and 3(b) show the measured electrical transport properties of the samples at 300 K. The n_H value marginally increased from 3.37 × 10¹⁸ cm^-3 to 4.11 × 10¹⁸ cm^-3 when a small amount of Se (~0.03 at. %) was doped to pristine Re₂Te₅ sample. However, n_H decreased with a further increase in Se content. The μ_H values of the samples measured at 300 K were 0.20, 0.18, 0.12, and 0.11 cm²/Vs for x = 0, 0.2, 1, and 2, respectively. The μ_H values decreased gradually as the Se content increased. The increase in σ for x = 0.2 and the decrease in σ for x = 1 and 2, were due to the improved n_H for the sample with x = 0.2, and the reduced n_H and μ_H for the samples with x = 1 and 2.

S as a function of n_H at 300 K is plotted for the series of samples (Pisarenko plot) in Figure 3(c). The dotted lines in Figure 3(c) indicate the contours of the density-of-state effective mass (m_d^*, expressed with respect to the free electron mass, m₀) according to the Mott relationship [26].

where h, e, and k are the Planck’s constant, elementary charge, and Boltzmann constant, respectively. Figure 3(d) shows the change in m_d^* of the Re₂Te_5-xSe_x (x = 0, 0.2, 1, and 2) samples with respect to x. As the Se content increased, the m_d^* value gradually decreased. The m_d^* values of the samples were 0.64, 0.63, 0.16, and 0.06 m₀ for the samples with x = 0, 0.2, 1, and 2, respectively.

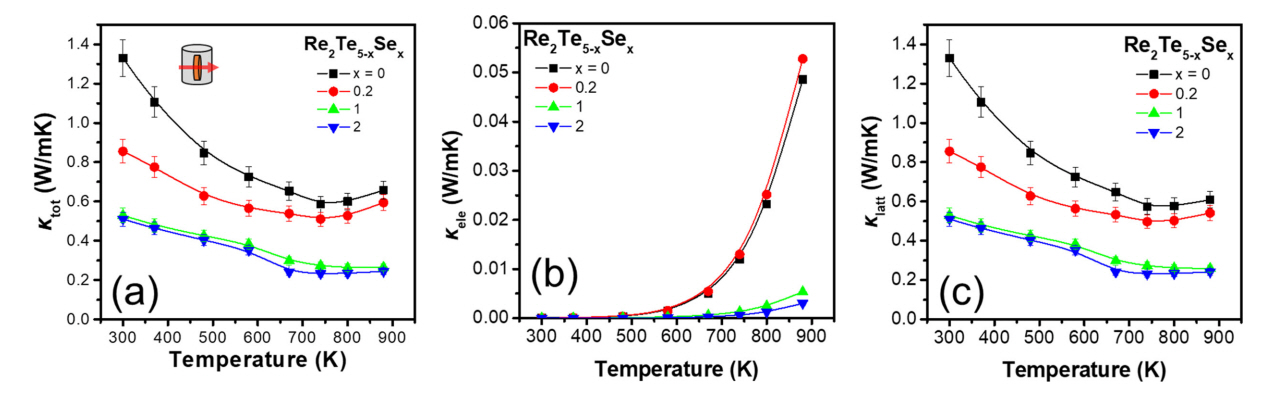
Figure 4(a) shows the plot of κ_tot vs temperature for the Re₂Te_5-xSe_x (x = 0, 0.2, 1, and 2) samples. The measured κ_tot value of the undoped sample gradually decreased with T from 1.33 to 0.59 W/mK up to 740 K, but then increased to 0.66 W/mK at 880 K. The κ_tot values of the doped samples were significantly low (below ~0.85 W/mK), and notably, the samples with x = 1 and 2 exhibited very low κ_tot values of 0.23-0.53 W/mK. Figure 4(b) shows the temperature dependence of κ_ele of the samples, and the κ_ele values exhibited a trend similar to that of the σ values. However, the influence of κ_ele on κ_tot was marginal, because the measured σ was less than 50 S/cm. Consequently, the κ_latt values were almost identical to the κ_tot values, as shown in Figure 4(c). Further, κ_latt gradually decreased with increasing Se content over the entire temperature range; this was attributed to the point defect phonon scattering by Se doping.

The gradual decrease in lattice parameters a, b, and c suggests an increase in lattice distortion, which leads to a decrease in κ_latt. Furthermore, the scattering parameters are proportional to the difference in mass (ΔM) in the pointdefect scattering mechanism [27]. Therefore, the difference between the atomic masses of Te (127.6 u) and Se (79.0 u) also contributed to the decrease in κ_latt.

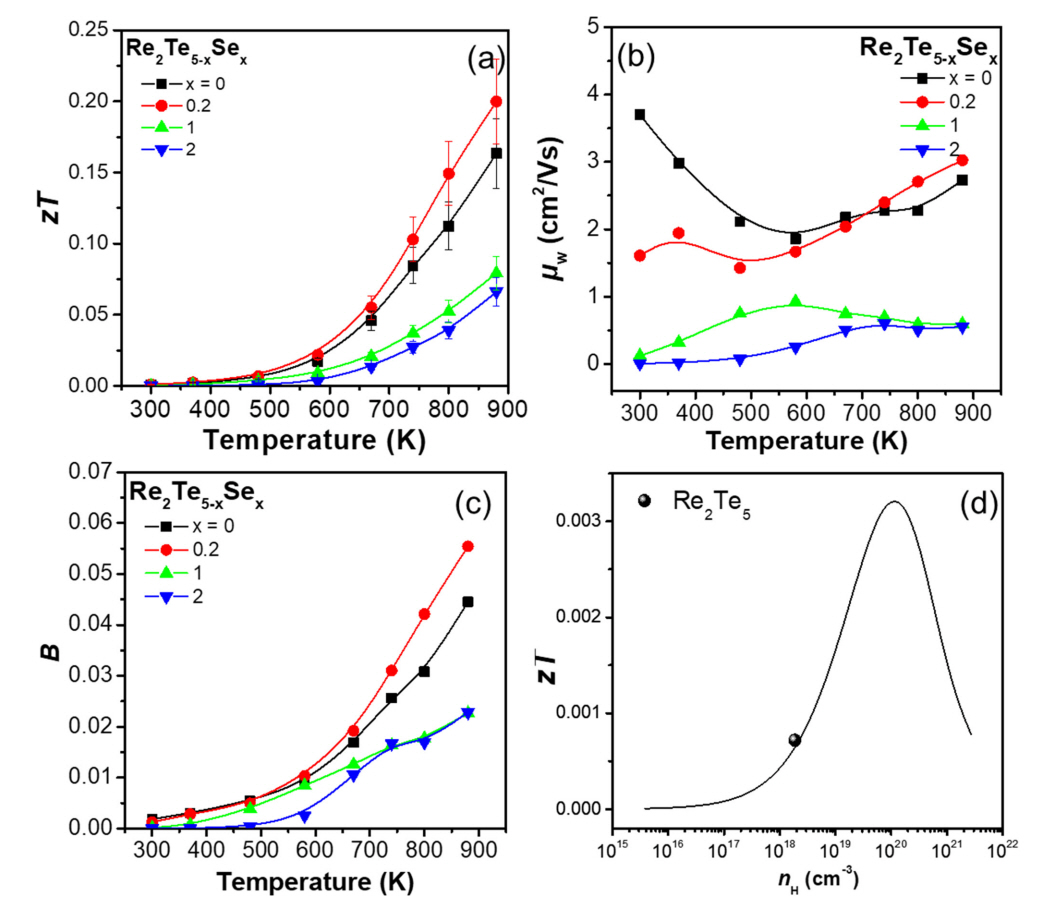
Next, the zT values were calculated using the measured σ, S, and κ_tot values of the samples (Figure 5(a)). The error margin for zT was less than 15%. The highest zT value of 0.20 was achieved for the sample with x = 0.2 at 880 K, which is ~22% higher than that of the pristine Re₂Te₅ sample. The zT enhancement for x = 0.2 was attributed to the marginal increase in PF and decrease in κ_tot. However, the other doped samples (x = 1 and 2) exhibited reduced zT values because of the significant decrease in PF, despite the very low κ_tot values.

Figure 5(b) shows the weighted mobility (μ_w) as a function of the temperature for the samples. μ_w is proportional to the maximum PF that a sample can reach when n_H is optimized. The μ_w value of each sample was calculated from the measured σ and S; μ_w can be obtained from a simple analytical form that approximates the exact Drude-Sommerfeld free-electron model given in Equation (2) for |S| > 20 μV/K [28].

where m_e is the mass of the electron. The calculated μ_w values at 880 K were 2.73, 3.03, 0.59, and 0.56 cm²/Vs for x = 0, 0.2, 1, and 2, respectively. The μ_w values increased at x = 0.2, and then decreased with increasing x, which is in agreement with the PF trend at 880 K. Therefore, the PF of the sample with x = 0.2 can be further improved by appropriate n_H tuning. In addition, μ_w is closely related to m_d^* as shown in Equation (3) [29].

where μ₀ is the non-dE_generate mobility. The μ_w values of the samples at 300 K were 3.70, 1.61, 0.12, and 0.08 cm²/Vs for x = 0, 0.2, 1, and 2, respectively. The μ_w values at 300 K decreased with x, which can also be observed in the m_d^* trend.

Figure 5(c) shows the dimensionless thermoelectric quality factor (B) of each sample, calculated from μ_w and κ_latt. B was calculated using Equation (4) [28]:

B is related to the maximum zT that a material can achieve when n_H is optimized. The general trend of B closely followed that of zT: B increased at x = 0.2, and decreased with a further increase in Se content. Figure 5(d) shows the plot of the expected zT of pristine Re₂Te₅ as a function of n_H at 300 K using a single parabolic band model. The parabolic line in Figure 5(d) was calculated using Equation (5) [29].

where F_xη (η is the reduced electrochemical potential) and τ_ac are the Fermi intE_gral and relaxation time of acoustic phonon scattering, respectively.

Therefore, maximum zT can be achieved when n_H is ~1020cm^-3. Accordingly, the zT of Re₂Te₅ can be substantially en_Hanced by appropriate cation doping, such as Zr⁴⁺, Sn⁴⁺ and Hf⁴⁺, in Re⁵⁺-site, considering the significant decrease in κ_tot due to Se doping.

A series of Re₂Te_5-xSe_x (x = 0, 0.2, 1, and 2) polycrystalline samples were prepared to investigate their electrical and thermal transport properties. Pure orthorhombic Re₂Te₅ phases were synthesized without any impurities, and the lattice parameters a, b, and c gradually decreased with increasing Se content, confirming the substitution of Se atoms at the Te sites. A maximum power factor of 0.135 mW/mK² was obtained for the sample with x = 0.2 at 880 K, predominantly due to the increase in the n_H and σ. The lattice thermal conductivity significantly decreased with increasing Se content, which was attributed to the point defect phonon scattering by Se doping. Further, zT reached a maximum value of 0.20 at 880 K for the Re₂Te_4.8Se_0.2 (x = 0.2) sample, an enhancement of approximately 22% compared to the pristine Re₂Te₅ sample. The single parabolic band model predicted that zT can be further improved by appropriate n_H tuning.