매트랩/시뮬링크 simulation model을 이용한 열전 모듈의 효율 예측
Method for Predicting Thermoelectric Module Efficiency Using MATLAB/Simulink
Article information
Trans Abstract
Development new high-performance thermoelectric materials for more efficient power generation systems and eco-friendly refrigerating systems has been challenging. Over the past few decades, thermoelectric studies have been focused on increasing the thermoelectric properties of materials. However, for conventional applications, developing of thermoelectric devices or modules with lower cost and simpler fabrication processes is also important. Simulation models that can predict the thermoelectric efficiency of modules using the thermoelectric properties of materials are needed for this purpose. In this study, we developed a simple model for calculating the efficiency of thermoelectric modules using MATLAB/Simulink. In this model, the temperature difference between the hot source and heat sink was fixed to ensure the precise comparisons of thermoelectric efficiency. The electric resistivity and Seebeck coefficient of thermoelectric materials was used in order to predict the efficiency of the thermoelectric modules. Then, the efficiency of the thermoelectric modules was verified using measured values which had been reported in prior experimental works. In this study, the simulated values were higher than the real thermoelectric effiency values. To address this, the simulations should consider the thermal resistance or electric contact resistance between the thermoelectric materials and electrodes.
1. 서 론
산업의 발달과 더불어 화석 연료의 사용이 급격히 증가하고 있으며, 현재까지도 화석 연료는 전 세계 에너지 사용량의 80%를 차지할 정도로 주된 에너지원으로 활용되고 있다. 그러나 환경 오염 및 기후 변화, 자원 고갈 등 화석 연료로 인한 문제가 심각해짐에 따라 친환경 에너지 기술 개발의 중요성이 커지고 있다 [1]. 다양한 친환경 에너지 기술 중 특히 열전 에너지 변환은 저소음, 친환경성, 정밀한 온도 제어와 같은 장점으로 인해 발전 [2-6] 및 냉각 [7-11] 시스템 분야에서 주목을 받아왔다. 열전 에너지 변환의 효율은 일반적으로 소재의 열전 변환 효율에 의해 결정되며, 이를 위하여 소재의 열전 성능 지수를 높이기 위한 다양한 연구가 진행되었다 [12-17]. 이와 더불어 열전 에너지 변환의 상용화를 위해서 필수적인 모듈의 제작 공정 기술 및 성능 예측 등을 위해서는 주의 깊은 모듈의 설계 및 재현성 확보를 위한 테스트 기술이 필요하다. 일반적인 열전 모듈(thermoelectric module, TEM)은 서로 다른 p형 및 n형 열전 소재를 교대로 전극층과 접합한 형태로 고체 상태에서 전기 에너지와 열 에너지를 가역적으로 변환할 수 있는 구조체이다. 열전 모듈에는 열전 발전 모듈(thermo-electrical generator, TEG)과 열전 냉각 모듈(thermo-electrical cooler/heater, TEC)로 나뉠 수 있다. 그 중에서 열전 발전 모듈은 온도 구배에 의하여 전위차가 발생하는 모듈이며, 열전 냉각 모듈은 전기 에너지를 온도 차이로 변환할 수 있는 모듈이다. 기본적으로 두 개의 서로 다른 반도체(n형 및 p형) 펠릿(pellet)을 전기적으로는 직렬로 연결하여 구동 전압을 증가시키고, 열적으로는 병렬로 연결하여 열 저항을 감소시키는 방법을 채택한다 [18-20]. 더불어 열전 모듈의 최대 전력은 부하 저항(load resistance)이 모듈 저항과 일치하고, 온도 구배가 클 때 이루어진다 [21]. 그러나 현재까지는 이러한 열전 모듈의 성능을 예측하기 위해서는 실제로 모듈을 만들어 측정을 해야 한다는 어려움이 존재하였다. 따라서 시뮬링크(Simulink) 와 같은 시뮬레이션 프로그램을 통해 실제 모듈 제작 및 테스트에 필요한 비용을 절감하고, 시간을 단축할 수 있다 [22-25]. Ronnie Andersson et al.은 시뮬레이션 프레임 워크(frame work)를 통하여 전기적으로 연결된 모듈의 전압과 전류 및 열 흐름(heat flow)을 예측하였고 실험적으로 약 97% 이상의 정확도를 보였다 [24]. 본 연구에서는 열전 모듈의 효율 모델링에 관한 문헌들에 제시된 조건들을 기반으로 하여 베이스 라인을 작성하였다. 양단에 온도를 설정하고, 재료의 전기 비저항 및 제벡계수를 입력하면 그에 따른 출력 전압(output voltage), 출력 전력(output power), 출력 효율(output efficiency)을 예측할 수 있는 모델을 설계하였으며, 실제 보고된 소재의 특성을 이용하여 그 예측을 검증하였다.
2. 이론 및 실험 방법
열전 모듈의 펠릿에서는 (1) 줄 발열(Joule heating), (2) 열 전도(thermal conduction, (3) 펠티어 발열 및 냉각(Peltier heating/cooling), (4) 제벡 효과(Seebeck effect), (5) 톰슨 효과(Thompson effect)가 일어나게 된다 [26]. 제벡 효과(Seebeck effect)란 온도 구배가 존재하는 폐회로(closed circuit)에서 재료의 고온부와 저온부 사이의 전위차이가 생성되는 현상을 의미한다 [27]. 열전 발전 모듈에서 온도 차 ΔT를 일정하게 유지하였을 때 발생하는 전기장 제벡 전압은 개방 회로에서의 전압과 같으며, 개방전압 VOC은 p, n형 제벡 계수와 온도 구배의 곱으로 나타낼 수 있다.
이 때 제벡 계수는 α = αp-αn, 온도 구배 ΔT = Th-Tc로 나타낼 수 있다.
열전 발전 모듈의 전기장은 N 쌍의 p-n 접합으로 이루어져 있기 때문에 전체 제벡 계수는 αtotal= Nα이며, 이에 따라 전체 기전력(Electromotive force)은 다음의 식과 같이 나타낼 수 있다.
펠티어 효과(Peltier effect)란 서로 다른 두 금속이 접합되어 있을 때, 양단에 전위차를 걸어주면 냉각 및 발열이 일어나는 현상을 의미한다. 열전 발전 모듈에서 펠티어 효과는 다음의 식과 같이 표현할 수 있다 [28].
여기서 Th/c는 각 고온부 및 저온부의 온도, I는 열전 재료를 통해 흐르는 전류이다. 줄 발열(Joule heating effect)란 도체에 전류가 흐를 때 열이 발생하는 현상을 의미한다. 이때 발생한 열량은 전류의 제곱과 저항의 곱에 비례한다.
열 전도(Thermal conduction effect)는 푸리에 법칙(Fourier’s law)이라고도 알려져 있으며, 열 전달율은 열 전도도와 온도 구배, 면적에 비례한다 [29]. 열전 발전 모듈에서의 열전도 현상은 다음의 식과 같이 나타낼 수 있다.
이 때 Ap(m2), An(m2)은 p-n 펠릿의 단면적, Lp(m), Ln(m)은 p, n 펠릿 각각의 길이, ρT, p(mK/W), ρT, n(mK/W)은 p, n 펠릿 각각의 열 전도 비저항(Thermal resistivity), x는 초기 위치에서부터 열이 전달된 길이를 나타낸다.
열전 발전 모듈을 구성하는 p, n 펠릿의 열 저항(thermal resistance) RT(Ω)과 비저항(electrical resistivity) RE(K/W)은 다음과 같이 나타낼 수 있다.
RE,p, RE,n은 p, n 펠릿 각각의 전기 저항이며, ρE, p, ρE, n은 각 p-type, n-type 반도체의 비저항을 의미한다. 더불어 고온부로 들어오는 열량 Qh과 저온부의 열량 Qc을 앞서 언급하였던 푸리에 법칙을 사용하여 다음과 같이 나타낼 수 있다.
위의 식은 단일 p-n 펠릿 쌍에 대한 열량을 나타낸 것이며, N 쌍의 p-n 펠릿들이 존재할 때 위의 식은 다음과 같이 표현할 수 있다.
고온부와 저온부의 열 차이는 열전 발전 모듈에 의해 발생하는 전력(electrical power) PTEM로 표현할 수 있다. RTEM, T = RT/N는 전체 열 저항이며 RTEM,E = NRE은 전체 비저항을 나타낸다.
위의 식을 통해 열전 발전 모듈의 출력 전압은 전기장과 회로 내부의 전기 저항으로 인한 전압 손실의 차이임을 알 수 있다. 그림 1은 열전 발전의 모듈 구조에 대한 모식도이다. 열전 발전 모듈은 N개의 펠릿 쌍으로 이루어져 있는데 이 때, 전기적으로는 직렬 연결, 열적으로는 병렬로 연결된 구조이다. 소자 내부에는 기본적으로 소자 자체의 내부 저항이 존재하고, 외부 저항을 인가할 수 있다. 따라서 열전 발전 모듈의 효율은 고온부의 전자들이 에너지가 낮은 저온부로 확산되며 양단 간에 전위차가 발생하게 되면 전류가 흐르게 되는 것이다. 이 때 발생한 전위차는 온도 구배에 비례하게 된다.
위의 식들을 바탕으로 하여 열전 발전 모듈의 발전 효율은 가해진 열에 대해 발생한 전력의 비로 표현할 수 있으며, 다음과 같은 식으로 나타낼 수 있다.
위의 수식들을 기반으로 시뮬링크를 연동하여 예측 모델을 제작하였다. 보통 열전 물질의 효율을 구하는 데 있어서 대부분 모듈 장비를 사용하며 전력 밀도(power density)와 전압(voltage)를 측정한다. 시뮬레이션의 경우 보통 하드웨어와의 연계를 통해 완성할 수 있지만 이는 정답이 존재하는 것이 아니므로 접촉 저항이나 열 손실, 열 복사 등과 같이 고려하는 매개변수에 따라서 신뢰도 및 완성도에 차이가 발생할 수 있다 [30-32]. 본 연구에서는 열전 모듈의 성능 예측을 위하여 매트랩(MATLAB) R2020a 버전을 사용하여 개방 전압과 출력 전력, 효율을 시뮬레이션으로 계산하였다. 시뮬레이션에 사용한 매트랩 프로그램은 대부분 내에 기본적으로 연동 되어있는 시뮬링크 블록(Simulink block)을 사용하였다. 그 중에서도 사용자 정의 기능 블록(User defined function block) 내 매트랩 시스템(MATLAB system)과 작업 공간(workspace) 연동을 시도하였다. 시뮬링크 모델에서 파라미터(parameter) 값을 설정하여 실험 환경을 구축하였고, 기초 데이터(raw data)를 바탕으로 부하 저항 및 전류에 따른 전압, 전력, 효율 값을 그래프로 작성하였다. 이를 통해 실제 모듈의 동작을 검증하고 필요한 결과 값을 추정하고 실험 시간을 단축할 수 있다. 열전 발전 모듈의 고정 조건 및 제어 조건을 표 1과 같이 정리하였다. 펠릿의 길이와 면적은 각각 1 × 10-4m, 1 × 10-7m2으로 설정하였다. 저온부 전극에서의 온도는 20 °C로 일정하게 설정하였으며, 고온부의 온도를 60 °C, 80 °C, 100 °C, 120 °C, 140 °C 조건 하에서 시뮬레이션을 수행하였다. 그리고 일반적으로 열전 발전 모듈에서는 발생한 기전력과 부하 저항에 의해 모듈의 전류 크기가 결정될 수 있다. 전류의 값에 따라 발전 모듈의 효율이 도출될 수 있으므로 부하 저항을 변화시켜 전류에 대한 전압, 전력, 효율 값을 구하고자 하였다. 열전 발전 모듈의 해석을 위하여 열전 모듈에 사용되는 n형 반도체와 p형 반도체의 조건은 각각 표 2와 표 3에 정리하였다. 제벡 계수와 비저항은 선행 연구에서의 실험치를 참고하였다 [33-35]. 편의를 위하여 그래프와 본문 상에서 n-type의 Bi2Te2.7Se0.3을 n1, Bi2Te2.7Se0.3-0.2 wt% 그래핀 산화물 복합체를 n2, Bi2Te3을 n3이라고 명명하였다 [33-34]. p-type의 경우, Bi0.42Sb1.58Te3을 p1, Cu0.01Bi0.42Sb1.58Te3을 p2라고 명명하였다 [35].
3. 결과 및 고찰
열전 발전 모듈에 대한 시뮬레이션 모델을 작성하여 부하 저항 및 전류에 따라 출력되는 전압, 전력, 효율 값을 구할 수 있었다. 측정 전압이 0이 되는 지점에서의 전류는 단락 전류(Isc)라고 하며, 측정 전류가 0이 되는 지점에서의 전압은 개방 전압(Voc)이라고 한다.
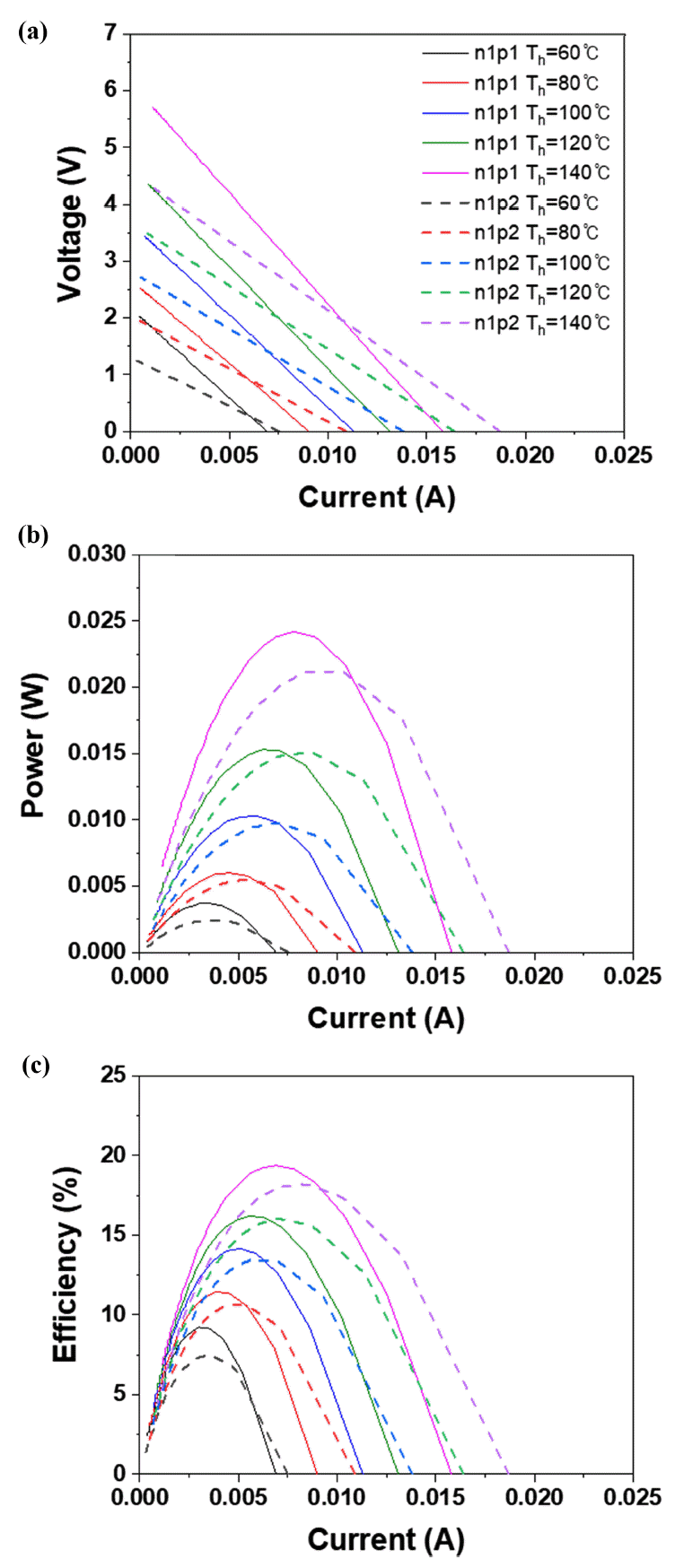
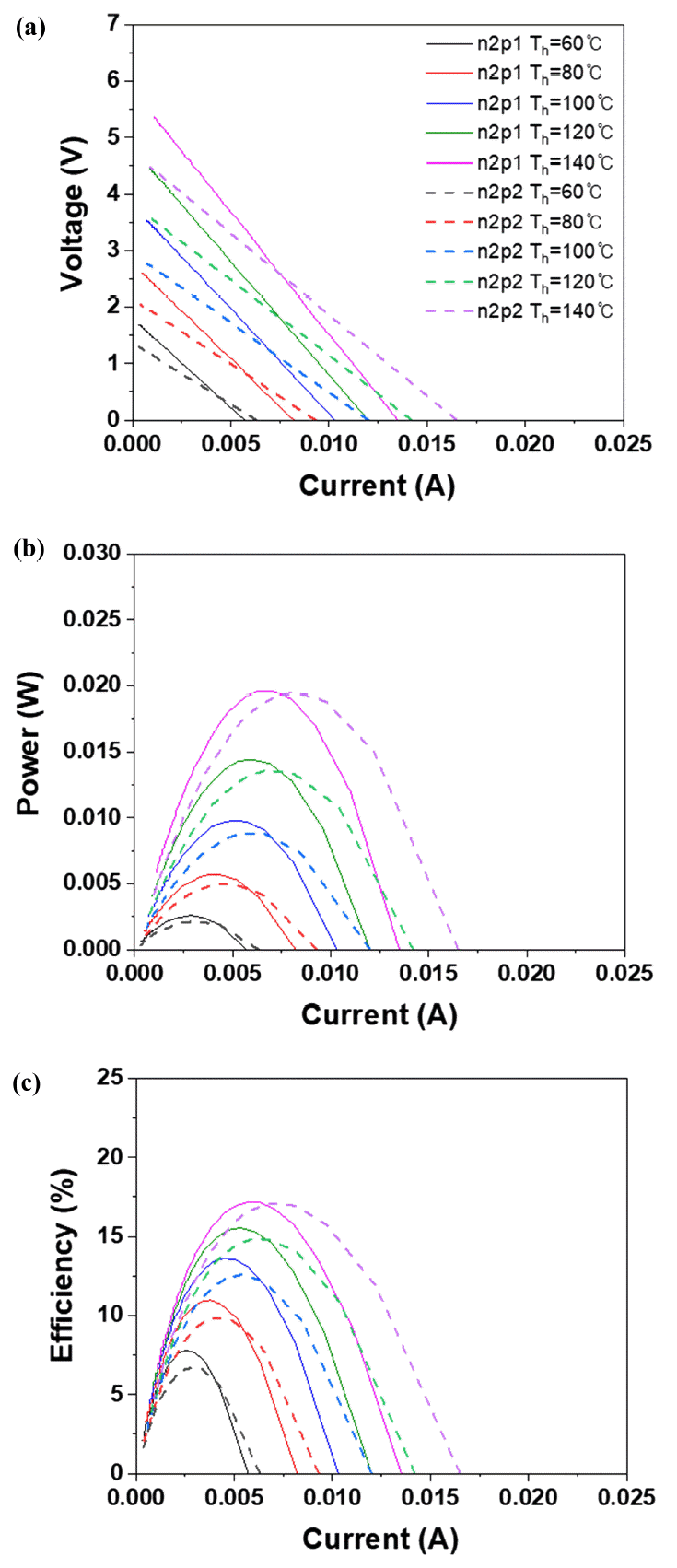
그림 2, 3, 4는 각각 n-type 조건 1, 2, 3에 대하여 ptype 조건 1, 2를 적용한 그래프를 나타낸 것이다. 그림 2, 3, 4의 (a)는 전류에 대한 개방 전압을 나타낸 것이다. 열전 소자의 양단에 온도차가 일정하게 유지될 때 제벡계 수가 높고, 비저항이 낮을수록 개방 전압의 기울기, 즉 저항이 낮게 나타난다. 또한 온도가 증가할수록 포화 전류가 증가하는 경향이 보이는데 이는 온도 증가로 인해 전자와 정공의 쌍(electron-hole pair)을 형성할 수 있는 캐리어의 양이 증가하기 때문이라고 사료된다 [36]. 그림 2, 3, 4의 (b)는 전류에 대한 출력을 나타낸 것이다. 출력 전력은 식 12와 같이 개방 전압과 전류, 저항에 대한 식으로 이루어져 있다. 소자의 양단에 온도 구배가 존재할 때 출력되는 전압을 제벡 전압(Seebeck voltage)라고 하며, 소자 내부에는 고유의 내부 저항이 존재하기 때문에 전류가 흐르게 된다. 따라서 열전 소자 자체에서 발생한 전압에 의해서 전류가 흐르게 되면, 전류가 소자의 내부를 흐르게 되면서 캐리어를 이동시키게 된다. 양단 간의 온도차가 증가하면 이동 캐리어가 증가하게 되면서 발생 전압도 높아진다. 그리고 온도차를 일정하게 유지하였을 경우, 주어진 열원 에너지가 일정하기 때문에 출력 전력이 전류에 비례하여 지속적으로 증가할 수 없다. 최대 전력(Pmax)는 단락 전류의 절반 지점에서 발생하며, 곡선형을 그리며 감소하게 된다. 이는 열전 소자 내부에서 발생한 전압에 의해 전류가 흐르게 되고, 캐리어를 이동시킴으로써 내부 저항이 발생하기 때문이다. 그림 2, 3, 4의 (c)는 전류에 대해 계산된 효율을 나타낸 것이다. 동일한 면적을 가지는 발전 모듈이라면 그림 2, 3, 4의 (a)에서 회로의 저항을 의미하는 기울기가 낮고, 단락 전류가 높은 경우에 모듈의 효율이 높다는 것을 알 수 있다. 본 연구에서 고려된 시뮬레이션 조건 중에서 가장 효율이 높은 조건은 n-type 조건 3번을 적용하였을 경우이다. 이는 비저항이 낮은 것이 효율에 더 큰 영향을 주는 것으로 나타났다.
실험적으로 n1과 n2는 그래핀 옥사이드(Graphene Oxide)가 각각 0.1, 0.2 wt% 첨가된 샘플로서 n2의 열전도도가 낮아 열전 성능지수가 증가하였다 [33]. 본 연구에서 n1-p1과 n2-p1 조건에 해당하는 시뮬레이션 결과를 비교하였을 때에도 n2-p1에서의 효율이 Th = 140 °C에서 약 36% 증가한 것을 알 수 있었다. p1은 Bi0.42Sb1.58Te3, p2는 p1 샘플에 Cu를 첨가한 Cu0.01Bi0.42Sb1.58Te3을 나타내며 p1 샘플은 p2보다 전기전도도가 낮다 [35]. 그림 2에서 n-type이 같은 조건일 때, p1과 p2 사이의 차이는 단락 전류에서 볼 수 있다. p1에서 온도에 따른 단락 전류는 각각 0.0069, 0.009, 0.0113, 0.0131, 0.0158 A였으며, p2에서의 단락 전류는 각각 0.0075, 0.0109, 0.0138, 0.0164, 0.0187 A를 나타내었다. 온도에 따른 p2의 단락 전류의 증가폭은 평균적으로 약 3% 더 높았다.
그림 5는 부하 저항에 따른 전압, 전력, 효율 그래프를 나타낸 것이다. 부하 저항은 조건은 0에서 0.01 Ω 범위 내에서 이루어졌으며, 0.001 Ω에서 최고 효율이 나타난 뒤 부하 저항이 증가할수록 출력 전력이나 효율이 감소하는 경향을 보였다. 시간이 지나면서 부하 저항이 증가하면 효율도 점차 감소하는 것이다. 이는 부하 저항이 증가할수록 열전 소재에서 발생하는 전압이 감소하게 되어 출력 전력을 낮추게 되고, 이는 식 (14)에서 표현된 것과 같이 출력 전력에 비례하는 효율 또한 감소하게 되는 관계를 가지게 되는 것이다. 온도차가 커질수록 부하 저항이나 전류에 따른 출력 값이 증가하는 경향을 보였다. 표 4는 열전 모듈 양 단의 온도 차이에 따른 최대 효율 시뮬레이션 결과를 나타낸 것이다. 이 때 주어진 조건 하에서 최소 6.68% 에서 최대 21.33%라는 결과를 나타내었다. 온도 구배가 가장 클 때, 최대 열전 효율이 높으나 기판과 펠릿 혹은 전선(Wire) 연결에서 발생하는 저항을 정확히 계산하기에는 어려움이 있으므로 모듈의 성능에 영향을 미치는 요인이 고려되어야 한다. 본 연구에서는 최소 40 °C에서 120 °C 범위의 온도 차를 설정하였고, 산업 폐열의 온도대와 비교하였을 때, 200 °C 보다 낮은 수준이다. Shakouri et al.은 zT가 0.5 이하인 열전 재료의 소자는 고온부의 온도가 1400K일 때 약 10%를 달성할 수 있는 것으로 발표하였다 [37]. 또한 Kumar Gaurav et al.은 약 275 °C의 온도차 조건에서 Bi2Te3 열전 발전 모듈의 효율은 약 7.10%로 계산하였으며 선행연구에서 진행한 실험치와 가까운 결과를 나타내었다 [38]. zT 값에 따라 열전 발전 효율이 달라질 수 있다는 점을 감안하더라도 다른 선행 연구들과 비교하였을 때 실제 효율보다 시뮬레이션에서 나타난 결과가 높음을 알 수 있다.

Load resistance VS voltage, current, power and efficiency (a), (c), (e), (g), (i), (k) at 60 °C, (b), (d), (f), (h), (j), (l) at 140 °C.
실제 모듈 제작 및 측정에 있어 기판과 펠릿 혹은 전선(Wire) 연결 등 실제 환경에서 발생하는 접촉부 저항이나 단차까지 정확히 고려하기에는 한계를 가지고 있으며, 이러한 공정상 오차로 인하여 형상의 변화, 펠릿의 제작의 최적화 요소 변화 등에 의하여 최대 효율에 영향을 미칠 수 있다 [39]. 전극을 연결하는 상하의 기판에서도 열 경계 조건이 존재하고, 이로 인한 전기적 손실이 발생할 수 있을 것으로 예측된다 [40]. 또한 개방 전압을 최대화하기 위해서 전체 면적에 대비하여 대면적을 차지할수록 전체 출력 효율이 높아질 수 있으나 현실적으로 시장 요구에 부합하는 수준의 집적도를 갖는 열전 발전 소자 제작에 한계가 존재한다. 집적도가 높아질 경우, 열전 소재와 전극 사이의 접촉 저항이 높아지기 때문에 전력 출력량이 낮아지게 된다. Lee et al. 은 면적이 4 × 4 cm2 인 모듈에 최대 114 EA/cm2의 집적도를 달성하였다 [41]. 그러나 전기 접촉 저항이 약 4.07 × 10-1 Ω·cm2으로 앞서 언급하였던 접촉저항 기준에 약 400,000배 높은 값을 가졌다. 이와 같이 실제 실험과 수치 해석에 기반을 둔 시뮬레이션간 차이점은 상기의 여러 가지 요인에 그 원인이 있을 것으로 사료되어진다. 이를 보완하기 위하여 소재의 개발부터 실제 하드웨어까지 연동하여 테스트를 진행하는 기법(Hardware-In-the-Loop)이나 연계 모의시험(co-simulation) 기법을 사용하는 연구도 보다 높은 신뢰성 확보를 위하여 적용할 수도 있을 것으로 예측된다 [42].
4. 결 론
현재, 높은 열전 성능지수를 갖는 물질에 대한 개발은 활발히 진행되고 있으나, 열전 재료 상용화를 위한 모듈화 및 재현성을 위한 기술 개발은 부족한 실정이다. 따라서 본 연구에서는 시뮬레이션 기법을 이용하여 n-type 및 ptype의 펠릿의 물성을 기반으로 전류에 대한 전압, 전력, 효율 값을 예측할 수 있는 모델을 연구하였다. 기존 선행연구를 통하여 확보한 n-type, p-type의 소재의 물성을 기반으로 본 연구를 통하여 개발된 시뮬레이션 모델을 활용하여 각각의 소재로 모듈을 만들었을 경우 기대되는 개방 전압 및 단락 전류를 비교 분석하였다. 이를 바탕으로 한 시뮬레이션 결과는 다른 선행 연구들과 비교하였을 때 실제 효율보다 높음을 알 수 있었는데, 이는 본 시뮬레이션에서 고려하기 힘든 열 저항, 접촉 저항 등이 그 원인이라고 사료된다.
Acknowledgements
This research was supported by “Human Resources Program in Energy Technology” of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) granted financial resource from the Ministry of Trade, Industry & Energy, Republic of Korea (No. 20194010000040), the National Research Foundation of Korea (NRF) Grant [NRF-2018R1D1A1A02085389] funded by the Korean government (MSIT), and the BK21 FOUR (Fostering Outstanding Universities for Research) funded by the Ministry of Education(MOE, Korea) and National Research Foundation of Korea (NRF) (NO.5199990214511).