1. Introduction
Tetrahedrite (Cu12Sb4S13) is an earth-abundant sulfosalt mineral composed of low-cost and eco-friendly elements, and lacks toxic elements such as Pb or Te. In addition, it has the characteristics of a p-type thermoelectric material and exhibits a high dimensionless figure of merit (ZT) at temperatures near 723 K [1-4]. The tetrahedrite has 58 atoms arranged in a complex crystal structure in a highly symmetrical cubic unit cell (space group 1 4 ¯ 3 m Cu 10 + Cu 2 2 + Sb 4 3 + S 13 2 -
Pi et al. [10] investigated the thermal stability, mechanical properties, and thermoelectric properties of Cu11TrSb4S13 (Tr = Mn/Fe/Co/Ni/Cu/Zn), and reported a ZT of 0.66 at 723 K for Cu12Sb4S13. Tippireddy et al. [11] studied the projected density of states, magnetic properties, and thermoelectric properties of Cu12-xTrxSb4S13 (x = 0.5 for Tr = Fe/Mn and x = 1 for Tr = Cu/Co/Ni/Zn) and obtained a ZT of 0.89 at 700 K for Cu11.5Mn0.5Sb4S13. In our previous studies, high ZT values were achieved for tetrahedrites by doping with transition atoms: ZT = 0.94 at 723 K for Cu11.8Co0.2Sb4S13 [12], ZT = 0.92 at 723 K for Cu11.8Ni0.2Sb4S13 [13], ZT = 0.80 at 723 K for Cu11.8Fe0.2Sb4S13 [14], and ZT = 0.76 at 723 K for Cu11.6Zn0.4Sb4S13 [15]. Chetty et al. [16] examined the elastic, magnetic, and thermoelectric properties of Cu12-xMnxSb4S13 (x = 0ŌłÆ1.8). As a result, they achieved a ZT of 0.76 at 623 K for Cu12Sb4S13, and among their Mn-doped samples, Cu11.6Mn0.4Sb4S13 exhibited the highest ZT of 0.64 at 673 K. Wang et al. [17] studied the thermoelectric properties of Cu12-xMnxSb4S13 (x = 0ŌłÆ2) and obtained a ZT of 0.89 at 700 K for Cu11.5Mn0.5Sb4S13. Gu├®lou et al. [18] analyzed the atomic displacement parameters to confirm the low-energy vibration of Cu atoms in Cu12-xMnxSb4S13 (x = 0 and 1) and achieved a ZT of 0.56 at 573 K for Cu11MnSb4S13.
Because the boiling temperature of S is lower than the melting temperature of Cu, the synthesis of tetrahedrite using a typical melting method requires a sophisticated heating-maintenance-cooling process and long-duration annealing (usually one to two weeks) to achieve phase transformation and homogenization [19,20]. However, mechanical alloying (MA) is a low-temperature process, and as a result, volatilization and segregation of component elements do not occur, which is advantageous for the homogenization of the synthetic phase [21]. In our previous study [22], we determined the optimal process conditions for synthesizing Cu12Sb4S13 with MA and hot pressing (HP), and a single tetrahedrite phase was obtained within 24 h without postannealing. In this study, Mn-doped tetrahedrites were prepared using the MA-HP method, and their charge-transport parameters and thermoelectric properties were examined.
2. Experimental Procedure
Mn-doped tetrahedrites Cu12-xMnxSb4S13 (x = 0.1, 0.2, 0.3, and 0.4) were synthesized by MA. Elemental powders of Cu (<45 ╬╝m, purity 99.9%, Kojundo), Mn (<45 ╬╝m, purity 99.9%, LTS), Sb (<150 ╬╝m, purity 99.999%, Kojundo), and S (<75 ╬╝m, purity 99.99%, Kojundo) were mixed in a stoichiometric ratio. Next, 20 g of the mixed powder and 400 g of 5 mm-diameter stainless steel balls were placed in a hardened steel jar. After the inside of the jar was evacuated, Ar gas was injected and MA was performed for 24 h at a rotation speed of 350 rpm using a planetary ball mill (Fritsch Pulverisette5). The synthesized powder was loaded onto a graphite mold, and HP was conducted at 723 K for 2 h under 70MPa in vacuum. Details of the MA-HP process have been reported in our previous study [22].
The phases of the hot-pressed specimens were analyzed using X-ray diffraction (XRD; Bruker D8-Advance) with Cu K╬▒ radiation (╬Ė-2╬Ė mode; step size: 0.02 ┬░; scan speed: 0.4 s/step). The lattice constant was calculated using the Rietveld refinement (TOPAS software). Scanning electron microscopy (SEM; FEI Quanta400) and energy-dispersive X-ray spectroscopy (EDS; Bruker Quantax200) were employed to observe the microstructures of the HP specimens. Through elemental mapping, the homogeneous distribution of the elements was confirmed. Charge transport parameters (Hall coefficient, mobility, and carrier concentration) were examined using the van der Pauw method (Keithley 7065) by applying a direct current of 100 mA and a constant magnetic field of 1 T. The electrical conductivity (Žā) and Seebeck coefficient (╬▒) were measured simultaneously in the temperature (T) range from 323 to 723 K using a Ulvac-Riko ZEM-3 system in He atmosphere. Thermal conductivity (╬║) was determined using the density, specific heat, and thermal diffusivity as measured by the Ulvac-Riko TC-9000H equipment. Finally, the power factor (PF = ╬▒2Žā) and dimensionless figure of merit (ZT = ╬▒2Žā╬║-1T) were evaluated.
3. Results and Discussion
Fig 1 presents the XRD patterns of Mn-doped tetrahedrite Cu12-xMnxSb4S13 specimens synthesized by the MA-HP process. All specimens contained only a single tetrahedrite phase without secondary phases. No significant change was observed in the lattice constant (1.0374ŌłÆ1.0379 nm) with a change in Mn content, as shown in Table 1. However, the lattice constant of doped samples increased compared to that of undoped Cu12Sb4S13 (1.0350 nm) [10]. This confirmed the successful substitution (doping) of Mn for the Cu sites, because the ionic radius of Mn2+ (66 pm) is larger than that of Cu+ (60 pm). Chetty et al. [16] reported an increased lattice constant of 1.043 nm for Cu10.2Mn1.8Sb4S13 compared to 1.032 nm for Cu12Sb4S13. Gu├®lou et al. [18] also obtained similar results of 1.0323 nm for Cu12Sb4S13 and 1.0386 nm for Cu11MnSb4S13, showing a significantly increased lattice constant due to Mn substitution. In this study, the amount of Mn substitution (x = 0.1ŌĆō0.4) was less than that used in other studies, and thus, the increase in lattice constant was not large.
Fig 2 displays SEM images of hot-pressed Cu12-xMnxSb4S13. No significant difference in microstructure with a change in Mn content was observed, indicating a densely sintered microstructure with few pores. As shown in Table 1, all specimens exhibited high relative densities of 98.6%ŌĆō99.8%, and there was no remarkable difference between the nominal and actual compositions. In particular, the composition change resulting from the volatilization of S, which is easily generated in the melting process, was suppressed. The EDS elemental maps showed that each element of Cu11.7Mn0.3Sb4S13 was homogeneously distributed. In this study, the volatilization of the component elements was suppressed, and compact sintering was successfully achieved using the solidstate MA-HP process.
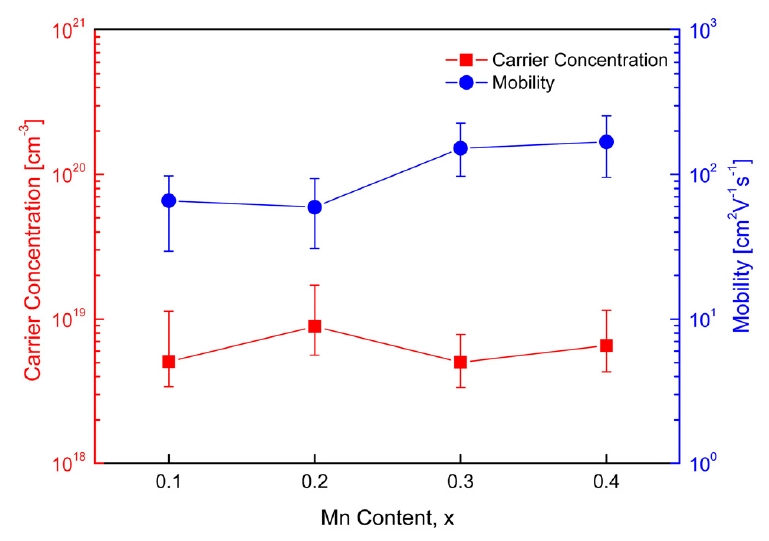
Fig 3 shows the carrier concentration and mobility of Cu12-xMnxSb4S13. The change in the carrier (hole) concentration according to the Mn content was not large. However, the mobility increased with increasing Mn content. When Cu was substituted by Mn, the additionally generated electrons did not meet the expectation that the carrier concentration would decrease due to a reduction in hole concentration (charge compensation). All specimens exhibited positive Hall coefficients, indicating p-type conduction. However, the Hall coefficient values measured in this study were unreliable because a different value was obtained for each measurement. Many studies have failed to effectively measure the Hall coefficient of tetrahedrite [3,11].
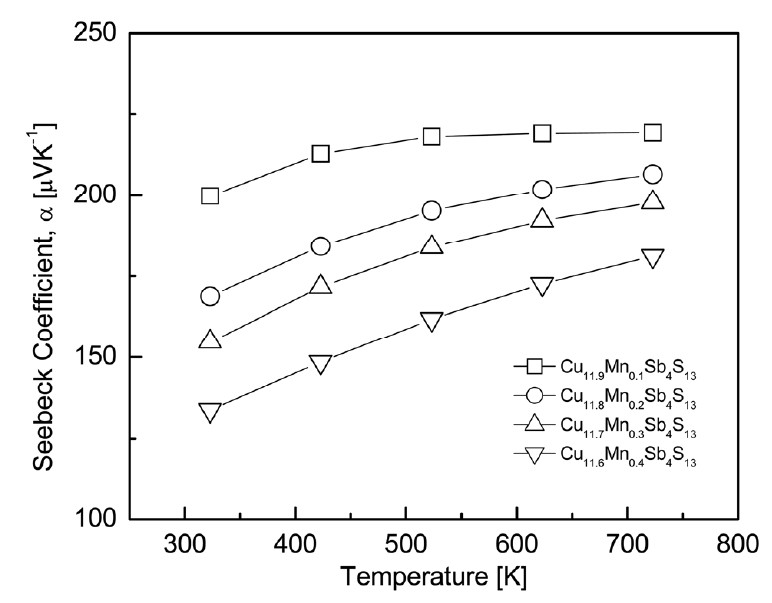
The thermoelectric properties of Cu12-xMnxSb4S13 were measured and examined in the temperature range of 323ŌĆō723 K. Fig 4 presents the Seebeck coefficient of Cu12-xMnxSb4S13. Positive Seebeck coefficient values were found for all specimens, suggesting that the major carriers were holes of p-type semiconductors. The Seebeck coefficient is expressed as the relation: ╬▒ = (8/3)ŽĆ2kB2m*Te-1h-2(ŽĆ/3n)2/3, where kB is the Boltzmann constant, m* is the effective carrier mass, e is the electronic charge, h is the Planck constant, and n is the carrier concentration [23]. The Seebeck coefficient increases as the temperature increases, but when the temperature exceeds a certain temperature (intrinsic transition temperature), the carrier concentration increases rapidly and thus the Seebeck coefficient decreases. As a result, the Seebeck coefficient of a p-type semiconductor decreases after showing a peak value at a specific temperature. In this study, as the temperature increased, the Seebeck coefficient increased for all specimens. This implied that no intrinsic transition occurred in the measured temperature range of 323ŌĆō723 K.
As the Mn content increased at a constant temperature, the Seebeck coefficient decreased and its temperature dependence greatly increased. Cu11.9Mn0.1Sb4S13 exhibited the highest Seebeck coefficient value of 200ŌĆō219 ╬╝VK-1 at 323ŌĆō723 K. This was higher than the 155ŌĆō195 ╬╝VK-1 at 323ŌĆō723 K for undoped Cu12Sb4S13 obtained by Pi et al. [10]. Therefore, the partial substitution of Mn at the Cu sites led to an increase in the Seebeck coefficient of tetrahedrite. However, it decreased to 134ŌĆō181 ╬╝VK-1 at the same temperature for Cu11.6Mn0.4Sb4S13. Chetty et al. [16] reported increased Seebeck coefficient values from 90ŌĆō142 ╬╝VK-1 for Cu12Sb4S13 to 96ŌĆō150 ╬╝VK-1 for Cu11.6Mn0.4Sb4S13, and 287ŌĆō400 ╬╝VK-1 for Cu10.2Mn1.8Sb4S13 at 300ŌĆō723 K with increasing Mn substitution. Wang et al. [17] obtained approximately three-times higher values of 250ŌĆō325 ╬╝VK-1 for Cu10Mn2Sb4S13 compared to 77ŌĆō134 ╬╝VK-1 for undoped Cu12Sb4S13 at temperatures from 300 to 700 K, and they interpreted the reason for the increased Seebeck coefficient: the carrier (hole) concentration decreased because the divalent or trivalent transition element was substituted at the Cu+ sites. In this study, although the Seebeck coefficient was increased by Mn doping compared to that of the undoped tetrahedrite, the reason why the Seebeck coefficient decreased with increasing Mn content is still questionable.
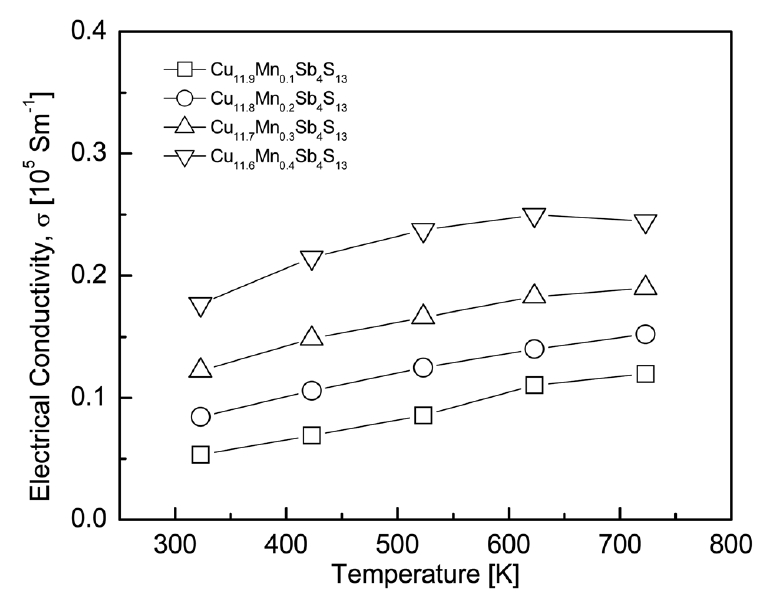
Fig 5 shows the temperature dependence of the electrical conductivity of Cu12-xMnxSb4S13. The electrical conductivity increased as the temperature increased and decreased slightly at temperatures above 723 K for only Cu11.6Mn0.4Sb4S13. This means that the Mn-doped tetrahedrites behave as nondegenerate semiconductors. The electrical conductivity at a constant temperature increased with increasing Mn content. In this study, the highest electrical conductivity values of (1.8ŌłÆ2.4) ├Ś 104 Sm-1 were obtained for Cu11.6Mn0.4Sb4S13 in the temperature range of 323ŌĆō723 K. These values were slightly higher than those for undoped Cu12Sb4S13, (1.1ŌĆō1.9) ├Ś 104 Sm-1 at 323ŌĆō723 K[10]. Mn doping resulted in the opposite trend of what was expected, a decrease in electrical conductivity owing to the decreased hole concentration. Chetty et al. [16] obtained electrical resistivities of 1.013 and 1.693 m╬®cm at 300 K for Cu12Sb4S13 and Cu11.6Mn0.4Sb4S13, respectively, with little dependence on temperature, and reported that the electrical resistivity increased (the electrical conductivity increased) to 181ŌĆō66 m╬®cm at 300ŌĆō723 K for Cu10.2Mn1.8Sb4S13. Wang et al. [17] obtained an electrical conductivity of (8.6ŌĆō6.5) ├Ś 104 Sm-1 at 300ŌĆō700 K for Cu12Sb4S13, a decrease with increasing temperature, and reported an electrical conductivity of 0.1 ├Ś 104 Sm-1 at 300 K for Cu10Mn2Sb4S13, a decrease with increasing Mn content with little temperature dependence.
Fig 6 presents the power factor (PF) of Cu12-xMnxSb4S13. Because carrier concentration affects both the Seebeck coefficient and the electrical conductivity, optimization of the carrier concentration is necessary to obtain a high PF value. In this study, the PF increased with increasing temperature within the measured temperature range because it did not exceed the intrinsic transition temperature. As the Mn content increased, the PF increased because the increase in electrical conductivity was dominant over the reduction in Seebeck coefficient by Mn doping. In the case of Cu11.6Mn0.4Sb4S13, despite having the lowest Seebeck coefficient, the highest PF values of 0.32ŌĆō0.80 mWm-1K-2 were obtained in the temperature range of 323ŌĆō723 K owing to its highest electrical conductivity. However, Mn doping was not effective at increasing the PF of tetrahedrite; Chetty et al. [16] obtained a maximum PF of 1.7 mWm-1K-2 at 623 K for Cu12Sb4S13, which decreased to 1.2 mWm-1K-2 at 623 K for Cu11.6Mn0.4 Sb4S13. Wang et al. [17] reported a maximum PF of 1.2 mWm-1K-2 at 700 K for Cu12Sb4S13, which decreased to 0.9 mWm-1K-2 at 675 K for Cu11.5Mn0.5Sb4S13.
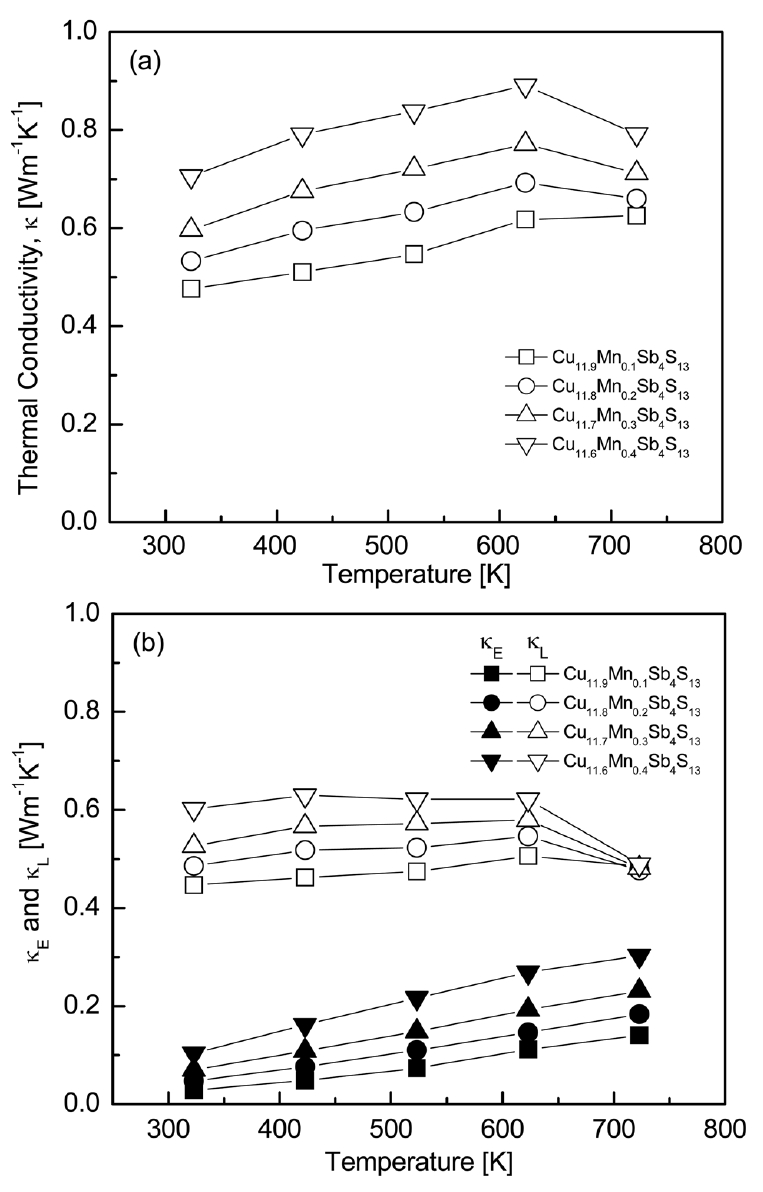
Fig 7 shows the temperature dependence of thermal conductivity of Cu12-xMnxSb4S13. The maximum total thermal conductivity of all specimens was observed at 623 K, and it increased with increasing Mn content at a constant temperature. The lattice thermal conductivity (╬║L) was calculated using the equation: ╬║L = ╬║ ŌłÆ ╬║E, where ╬║ is the total thermal conductivity and ╬║E is the electronic thermal conductivity. The ╬║E was estimated using the WiedemannŌĆōFranz law (╬║E = LŽāT, L: Lorenz number) [24], where the Lorenz number [10-8 V2K-2] was obtained using the formula [25]. As shown in Table 1, as the Mn content increased, the Lorenz number increased from 1.68 ├Ś 10-8 to 1.82 ├Ś 10-8 V2K-2 at 323 K. The electronic thermal conductivity increased with increasing temperature, but the total thermal conductivity increased with increasing temperature, reached a maximum at 623 K, and then decreased. This was due to the combined result of increasing electronic thermal conductivity with increasing temperature and decreasing lattice thermal conductivity at temperatures higher than 623 K. The electronic thermal conductivity was directly related to the electrical conductivity (carrier concentration) and Lorenz number, and thus, it increased with increasing Mn content. Cu11.9Mn0.1Sb4S13 exhibited the lowest lattice thermal conductivity, resulting in the lowest total thermal conductivity of 0.48ŌĆō0.63 Wm-1K-1 at 323ŌĆō723 K, where ╬║E = 0.03ŌĆō0.14 Wm-1K-1 and ╬║L = 0.45ŌĆō0.49 Wm-1K-1.
The dimensionless figure of merit (ZT) of Cu12-xMnxSb4S13 is presented in Fig 8. As the temperature increased, the ZT value increased because of the increase in the PF and the maintenance of low thermal conductivity. In our previous study [10], undoped Cu12Sb4S13 exhibited a ZT of 0.66 at 723 K. In this study, as the Mn content increased, both the thermal conductivity and PF increased. As a result, Cu11.7Mn0.3Sb4S13 exhibited the highest ZT of 0.75 at 723 K. Wang et al. [17] reported a ZT of 0.89 at 700 K for Cu11.5Mn0.5Sb4S13 prepared by encapsulated melting and HP. Gu├®lou et al. [18] obtained a ZT of 0.56 at 573 K for Cu11MnSb4S13 produced by MA and HP. Wang et al. [17] performed long-term and careful melting processes; raw elements were heated to 923 K, maintained for 12 h, cooled to room temperature, and then annealed at 723 K for two weeks. Gu├®lou et al. [18] also conducted long-term and multi-step processes; samples were mechanically alloyed for 6 h, annealed at 973 K for 3 h, and cooled to 823 K for 30 h. The furnace was then cooled to room temperature, and finally, the ingot was crushed and subjected to a second annealing at 823 K for 30 h. In the present study, however, a single tetrahedrite phase exhibiting a high level of ZT was obtained by MA within 24 h without post-annealing. Therefore, the MA-HP process is suitable for preparing doped tetrahedrites with excellent thermoelectric performance.
4. Conclusions
Mn-doped tetrahedrites Cu12-xMnxSb4S13 (x = 0.1ŌłÆ0.4) were synthesized by MA, followed by HP. The hot-pressed specimens had a relative density higher than 98.6%. Positive Hall and Seebeck coefficient values were obtained, meaning that all of the Mn-doped tetrahedrites acted as p-type semiconductors. As the temperature increased, the Seebeck coefficient and electrical conductivity increased. As the Mn content increased, the Seebeck coefficient decreased but the electrical conductivity increased. The trend in electronic thermal conductivity was the same as that of electrical conductivity, and the minimum thermal conductivity was achieved for Cu11.9Mn0.1Sb4S13. The PF increased because of the increase in electrical conductivity with increasing Mn doping level. As a result, the maximum ZT value of 0.75 was obtained at 723 K for Cu11.7Mn0.3Sb4S13.